원제 : Linear Regression의 쉬운 풀이 - 1 -
Ridge와 Lasso Regression을 이해하기 위한 Preview
Keywords
#예측모형, #선형회귀모형, #linearregression, #costfunction, #GradientDescent, #R-squared, #AdjustedR-squared, #Python
개요
대형 슈퍼마켓의 operations manager로 일하는 친구와 얼마 전 이야기를 나누었습니다. 대화 중 우리는 명절 전 슈퍼마켓의 재고 준비 정도에 대해 이야기를 이어갔습니다. 그는 어떤 물건이 그 시기에 가장 잘 팔릴지, 그리고 어떤 물건은 그렇지 않을지를 예측하는 것이 매우 중요하다고 이야기했습니다.
만약 매니저가 잘못된 선택을 한다면 친구의 상점을 방문한 고객들은 근처 경쟁 상점으로 가서 물건을 구매할테니까요. 문제는 여기서만 끝나는 게 아닙니다. 매니저로서 소비자의 각자 다른 소비 행태들을 예상하여 물건 배치를 어떻게 구성해야 할지도 예측해야 합니다.
친구가 이 문제를 설명하고 있을 때, data scientist인 저는 오늘 주제를 regression model로 다루고 어떻게 그 모형으로 친구의 문제를 해결할 수 있을지 설명해야겠다 마음 먹었습니다.

간단한 예시로 brainstorming을 해봅시다.
잠시 시간을 가지고 친구 상점의 판매량에 영향이 있을 만한 모든 변수들을 써보세요. 그리고 각각의 변수에 따라 왜 그리고 어떻게 해당 변수가 판매량에 영향이 미칠지 가정을 만들어보십시오. 예를 들어 저는 상점의 위치가 판매량에 강한 영향을 미칠 것이라고 생각합니다. 왜냐하면 지역 주민들은 각자 다른 라이프스타일을 살고 있기 때문이죠. 주민(가구원 수)이 더 많은 동네일수록 쌀의 판매량이 늘어나는 것처럼요.
이와 유사하게 가능하다고 생각되는 모든 변수를 써보세요.
상점의 위치, 물건보유여부, 상점의 크기, 세일 여부, 홍보, 상점 안에서의 물건 위치 등이 매출에 영향을 미치는 변수들이라고 생각됩니다.
데이터셋을 보여드리겠습니다. - The Big Mart Sales. 이 데이터는 다양한 아웃렛의 판매 정보입니다.

데이터셋을 보시면 우리는 팔린 물건에 대한 특징들(fat content, visibility, type, price)을 볼 수 있습니다. 그리고 아웃렛에 대한 특징(year of establishment, size, location, type)과 특정 아이템이 몇개 팔렸는지도 알 수 있습니다. 이제 이 변수들을 통해 매출액을 예상할 수 있을지 알아봅시다.
-------------------------------------------------------------------------------
[목차]
1. Simple models for Prediction
2. Linear Regression
3. The Line of Best Fit
4. Gradient Descent
5. Using Linear Regression for Prediction
6. Evaluate your Model - R square and Adjusted R squared
7. Using all the features for Prediction
8. Polynomial Regression
9. Bias and Variance
10. Regularization
11. Ridge Regression
12. Lasso Regression
13. ElasticNet Regression
-------------------------------------------------------------------------------
1. Simple models for Prediction
쉬운 방법으로 시작해봅시다. 제가 만약에 여러분에게, '상품 판매량을 예측하는 가장 간단한 방법은 무엇일까요?'라고 물어본다면 무엇이라고 대답하시겠습니까?
Model 1 - 평균 판매량:
머신러닝에 대한 지식이 없어도, 만일 어떤 item의 판매량을 예측해야 한다면 당신은 최근 며칠간/몇 달 간/몇 주 간 해당 item의 평균 판매량으로 계산할 것입니다.
좋은 시작이지만, 여기서 몇 가지 질문들도 추가됩니다. 모델이 얼마나 정확한가 입니다. 우리가 생성한 모형의 성능이 얼마나 좋은지는 여러 가지 방법으로 맞힐 수 있습니다. 가장 흔한 방법이 MSE(Mean Squared Error)입니다. 그럼 MSE를 어떻게 측정하는지 알아봅시다.
Predictoin error(예측 오차)
모형이 얼마나 좋은지 평가하기 위해서는 틀린 예측이 어떤 영향을 주는지 알아야 합니다. 우리가 만일 실제보다 더 큰 판매량을 예측한다면, 상점은 불필요한 재고 생성과 정리로 많은 돈을 손해 보게 됩니다. 반대로 예상한 판매량이 너무 적다면, 우리는 명절을 맞이하여 많이 벌 수 있는 그 기회를 놓치게 됩니다.
따라서 error를 계산하기 위한 가장 간단한 방법은, 실제값과 예측값의 차이를 계산하는 것입니다. 하지만 단순히 error를 더하기만 한다면 그 의미가 상쇄되는 경우가 있기 때문에 우리는 error값을 더하기 전 각 에러에 대한 값을 제곱(sqaure)합니다. 제곱된 에러의 합을 데이터 수(record)만큼 나눠 줌으로써 데이터 수에 따른 bias를 제거 합니다.
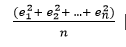
이것이 MSE입니다.
여기에서 나오는 e1, e2 …. , en 은 실제값과 예측값의 차이 입니다.
그렇다면 우리의 첫번째 모델에서 MSE는 무엇일까요? 모든 data points들의 평균값을 예측하면, MSE값은 2,911,799입니다. 굉장히 큰 에러처럼 보이긴 합니다. 어쩌면 평균값으로 예측한다는 것은 썩 좋지 않은 방법인 것 같네요.
그렇다면 에러를 줄이기 위해 어떻게 해야할지 생각해봅시다.
Model 2 - 지역에 따른 평균 판매량:
우리는 지역이 물건 판매량에 지대한 영향을 끼친다는 것을 알고 있습니다. 예를 들어 Delhi라는 도시가 Varanasi라는 도시보다 더 많은 자동차 판매량을 보인다고 해봅시다. 그렇다면 우리는 데이터의 column 중 'Outlet_Location_Type'을 쓰게 되겠죠.
그렇다면 각각의 location type의 평균 매출량을 계산하고 그에 맞게 예측을 한다고 해봅시다. 매출 판매량의 예측에 대한 MSE는, Model 1에서의 결과값보다 작은 2,875,386가 나오게 됩니다. 그렇다면 우리는 '지역'이라는 특성이 error값을 줄여줬다라는 것을 알 수 있게 되는 것입니다.
그렇다면 판매량이 여러 개의 변수들에 의해 영향 받는다면, 우리는 이 정보들을 이용해서 어떻게 판매량을 예측할 수 있을까요? 이런 문제를 해결하기 위해 Linear regression이 등장합니다.
2. Linear Regression
Linear regression은 예측 모델링에 있어서 가장 간단하면서도 많이 쓰이는 방법론입니다. 판매량은 target 변수가 되고, 앞서 이야기했던 여러 개의 변수들은 independent variables가 되는 것이지요.
그렇다면 공식으로는 어떻게 표현할까요? 이는 다음과 같습니다.
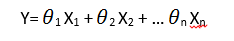
Y는 dependent variable(즉, 판매량)이 되고, X는 independent variables고 theta값은 각 X값에 해당하는 계수가 됩니다. 계수는 X변수의 중요도에 따라 그 가중치(weights)가 주어지게 됩니다.
예를 들어 변수들 중 '지역'이 '매장의 크기'보다 판매량에 더 큰 영향을 미친다고 가정해봅시다. 이 뜻은 Tier 1도시에 있는 작은 매장이 Tier 3에 있는 큰 매장에 비해서 더 높은 판매량을 기록한다는 것입니다. 그렇다면 '지역'에 해당하는 계수가 '매장의 크기'보다 더 높을 것입니다.
우선, 선형 회귀를 1개의 변수만으로 이해해 봅시다. 공식으로 나타낸다면 다음과 같겠습니다.

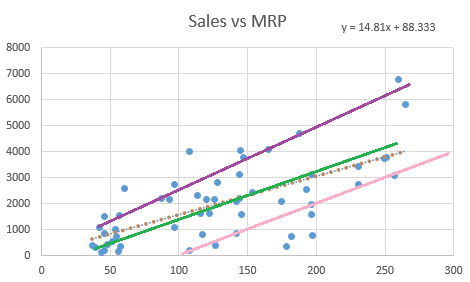
이 공식을 단순선형회귀(simple linear regression)라 부르고, ‘Θ0’ 이 절편이고, ‘Θ1’ 이 기울기인 일직선의 선을 뜻하는 것입니다. 다음과 판매량과 MRP와의 관계입니다.

놀랍게도 MRP가 증가함에 따라 판매량이 증가합니다. 따라서 빨간 점선은 regression line 또는 line of best fit을 표현합니다. 이때 질문이 있으시겠죠? 어떻게 이 점선을 찾을 수 있을까요?
3. The Line of Best Fit
아래 그림을 보면 MRP에 따른 판매량 예측을 표현하는 선은 무수히 많을 수 있습니다. 그렇다면 여기서 가장 적합하게 들어맞는 line은 어떻게 찾을까요?
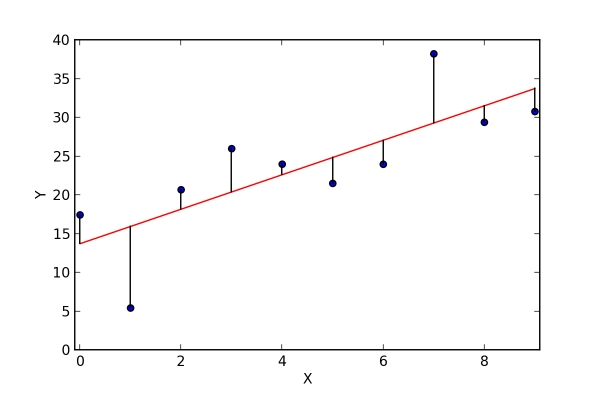
best fit line의 메인 목적은 우리의 예측값이 실제값과 그 거리가 될 수 있으면 최대한 작게 나게 하는 것입니다. 굳이 실제 값과 굉장히 차이나는 예측값을 찾을 필요는 없겠지요? 우리는 예측을 통해 나온 값과 실제 값의 차이를 줄이려 부단히 노력할 것입니다. 그리고 이 차이를 error라고 표현하죠.
그림으로 나타낸 error의 모습은 아래와 같습니다. 이 error값들은 residuals(잔차)라고도 표현됩니다. residuals는 예측값과 실제값의 거리를 나타내는 수직선입니다.
네, 이제 우리의 주요 목적이 error를 최소화하려는 것인 건 아시겠죠? 하지만 그전에 error 계산법에 대해 짚고 넘어갑시다. 제가 지금까지 error란 예측값과 실제값의 차이라고 계속 언급했습니다. 이 에러값 계산을 3가지 방법으로 나눠 봅시다.
ㆍ잔차의 합(Sum of residuals) (∑(Y – h(X))) – 양수와 음수의 값이 있다면 서로가 값을 상쇄하는 일이 발생할 것입니다.
ㆍ잔차의 절대값의 합(Sum of the absolute value of residuals) (∑|Y-h(X)|) – 절대값을 취하면서 값 상쇄 문제는 해결이 됩니다.
ㆍ잔차의 제곱의 합(Sum of square of residuals) ( ∑ (Y-h(X))^2) – 이 방법을 현재 우리가 가장 많이 활용합니다. 높은 에러값을 나타내는 점에 패널티를 부여함으로써 큰 에러와 작은 에러의 차이를 구분하는 것이지요.
잔차의 제곱의 합(Sum of square of residuals) 은 다음과 같이 나타낼 수 있습니다.

여기서 h(x)는 우리의 예측값입니다. h(x) =Θ1*x +Θ0 와 같이 표현될 수 있겠지요. y는 실제 값이고 m은 training set의 열의 수(즉 레코드 수)입니다.
*training set은 이전 글에서 설명을 드렸으니, 참고하시기 바랍니다. (딥러닝과 머신러닝 "이래서 다르구나")
The Cost Function(비용 함수)
매장의 크기를 늘리면 판매량이 증가한다는 것을 들은 당신은 더 큰 판매량을 달성하기 위해 매장의 크기를 늘리는 시도를 했다고 가정 해봅시다. 하지만 안타깝게도 판매량에서는 그렇게 큰 효과를 보지 못했습니다. 따라서 매장을 늘림으로써 발생하는 비용은 결국 음수의 값을 나타냈습니다.
그렇다면 이제 우리에게 주어진 과제는 비용을 줄이는 일입니다. 따라서 모델의 error값을 정의하고 측정하는, cost function(비용 함수)를 설명해드리겠습니다.
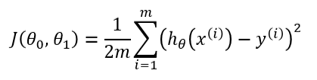
이 공식을 자세히 보시면, sum of squared errors와 굉장히 유사합니다. 앞에 1/2m을 곱해주는 것만 제외한다면요.
따라서 우리의 예측 성능을 개선시키려면 우리는 cost function을 최소화시켜야 합니다.
이러한 이유로 우리는 gradient descent algorithm을 이용하는 것입니다.
어떤 방식으로 작동이 되는 것인지 다음 장에서 알아봅시다.
*본 글은 https://www.analyticsvidhya.com/blog/2017/06/a-comprehensive-guide-for-linear-ridge-and-lasso-regression/의 일부분을 번역+약간의 의역을 하였습니다. 중간중간 저의 개별적인 설명은파란색 글씨로 써두었습니다.
<외부 기고 콘텐츠는 이웃집과학자 공식 입장과 다를 수 있습니다>
월급쟁이(hwpark0502@gmail.com)
늘 재밌게 살고싶은 월급쟁이의 데이터 이야기
원문 출처 : https://brunch.co.kr/@itschloe1/9

