<이웃집과학자>는 이번에 필진을 새로 모집했습니다. 전문가들 뿐만 아니라 비전문가들에게도 문호를 개방했는데요. 과학 자체를 좋아하고 자신이 관심 있는 분야에 대해 글을 작성해 <이웃집과학자> 이웃님들과 공유하고 싶어하는 학생들이 많았기 때문입니다. 다들 실력과 열정을 겸비한 멋진 분들인데요. 이런 점 감안해 학생들의 콘텐츠는 너그럽게 봐주시면 좋을 것 같습니다. -편집자 주
지난 1987년, 태풍 셀마가 대한민국을 강타한 사건이 있었습니다. 매년 여름마다 오는 태풍이지만 피해 규모는 사망·실종 345명, 이재민 10만 명, 재산 피해 약 6000억 원으로 매우 컸는데요. 그 이유는 기상청에서 이번 태풍은 우리나라를 관통하지 않을 거라는 오보를 했기 때문입니다. 태풍에 대한 대비가 전무했습니다. 이런 큰 사건이 아니더라도 많은 분들이 기상청의 오보 때문에 피해를 본 경험이 있을 겁니다. 그런데 기상전문가들이 모인 기상청에서 왜 이렇게 정확도가 낮은 예보를 할 때가 많은 걸까요?
작은 변수로도 큰 변화
기상 예보는 사실 굉장히 어려운 일입니다. 다양한 변수가 관여하는 복잡한 상황에서는 아주 작은 변수의 변화로도 이후의 결과가 매우 달라질 수 있다는 ‘카오스 이론’도 기상 시뮬레이션을 돌리던 과정에서 발견됐습니다. 1961년, MIT에서 기상학을 연구하던 에드워드 로렌츠는 기상 시뮬레이션을 돌리다가 시뮬레이션에 들어갈 숫자들을 소숫점 셋째 자리에서 반올림해서 넣었습니다. 그 정도 오차라면 시뮬레이션 결과에 별 차이가 없을 거라고 생각했기 때문이겠지요. 하지만 그는 곧 반올림한 숫자로 계산을 했을 때의 시뮬레이션 결과와 원래 숫자로 시뮬레이션을 했을 때의 결과가 완전히 다르다는 사실을 알게 됐습니다. 그는 이런 놀라운 결과에 대해 더 연구한 후, 1963년 <deterministic nonperiodic flow>라는 논문을 발표했습니다.
이 논문에서, 로렌츠는 3개의 변수를 가진 3개의 미분방정식의 초깃값을 여러 형식으로 바꾸면서 결과가 어떻게 초깃값에 따라 바뀌는지 살펴보았습니다. 로렌츠가 사용한 3개의 미분 방정식은 아래와 같습니다.
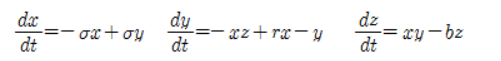
여기서 x는 속도의 진폭을, y는 상승하는 난류의 흐름과 하강하는 흐름의 온도 차이를, z는 온도를 나타내는 변수입니다. 또, 시그마는 운동량과 열의 확산 비율을 뜻하는 상수이고, b는 대류가 일어나는 단위세포의 수평 파수(단위길이당 파동이 몇 라디안만큼 진행하는지 나타냄)를 a라고 할 때 4/(1+a^2)라고 표현됩니다.
이 세 방정식은 특정한 단위세포에서 난류가 어떻게 흘러가는지를 매우 단순하게 나타낸 것인데요. 난류는 수많은 변수들이 관여하는 현상이지만 이 3개의 변수만으로도 꽤 놀라운 결과를 얻을 수 있습니다. 일단 안정한 상태로 수렴하는 경우들에 대해 계산을 해 봅시다.
안정한 상태로 수렴하는 경우는 아래와 같은 두 가지가 있습니다.

참고로 첫 번째 식은 열이 유체의 흐름 없이도 전달될 수 있는 현실에서는 있기 힘든 상황을 의미합니다. 이런 경우에는 아래 그림처럼 유체가 한 방향으로만 흐르는 상황이 만들어지지요. 물론 이렇게 숫자가 깔끔하게 맞아 떨어지는 경우는 현실에서 매우 찾아보기 힘들어요. 현실에서 이런 상황이 쉽게 발생했다면 지금보다 훨씬 정확한 일기예보를 들을 수 있겠지요.
그 다음에는 로렌츠가 했듯이 위의 미분방정식들에 σ = 10 (물이 가지는 실제 값이라고 합니다!), b = 8/3를 대입하고 r > 24.74여야 안정한 상태로 수렴하지 않기 때문에 임의로 r = 28을 대입해 봅시다. 또, 초깃값으로 (x, y, z)=(0, 0, 0)을 대입합시다.
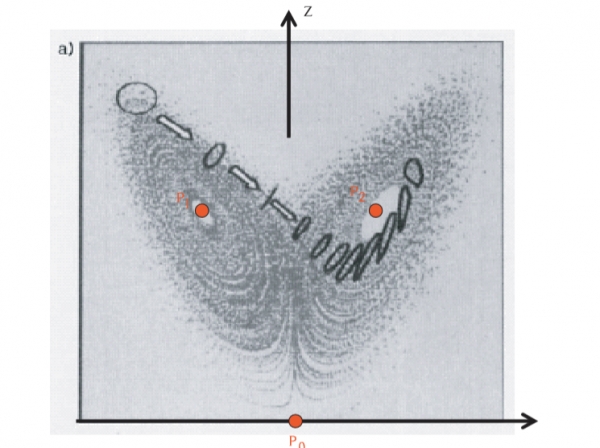
보시다시피 나비 모양의 복잡한 그래프를 얻을 수 있지요. 그림에서의 경우에는 한쪽 날개의 점으로 초기값을 잡았을 때 이후의 함수값이 한쪽 날개를 지나 반대쪽 날개에서 원을 그리고 다시 처음 출발한 날개로 돌아오는 것을 반복하고 있습니다. 이 경우에는 절대 초기값으로 수렴할 일이 없겠죠. 안정한 점도 절대 지나치치 않고요.
이 그래프에서 초기값을 약간 다르게 잡은 경우에 대해 살펴보도록 합시다.

첫 번째 그래프는 아까 봤던 그래프와 같은 상황이고, 두 번째 그래프는 그 그래프에서 초기값을 아주 조금 변화시킨 경우입니다. 마지막 그래프는 한쪽 날개에서 초기값을 잡았던 위의 두 경우와는 달리 두 날개 사이에서 초기값을 잡았을 때 함수값의 변화를 나타낸 그래프입니다.
첫 번째 그래프는 아까 설명한 것처럼 한쪽 날개에서 다른 쪽 날개로 함수값이 옮겨가지만 두 번째 그래프는 초기값이 비슷함에도 불구하고 반대쪽 날개로 함수값이 넘어가는 대신 두 나비 날개 사이로 값이 이동하는 모습을 볼 수 있습니다. 마지막 그래프는 초기값이 완전히 다른 경우이기에 함수값의 변화 양상 역시 당연히 다를 수밖에 없지요. 그렇지만 두 번째 그래프와는 조금 유사한 것 같습니다.
이처럼 초기값이 약간만 달라도 완전히 다른 형태의 결과를 얻을 수 있습니다. 초기값이 완전히 달라도 비슷한 모양의 그래프를 얻을 수도 있고요. 3개의 변수만으로도 이런 결과를 얻을 수 있는데, 현실에서처럼 수십개의 변수가 관여하는 경우에는 정말 미래를 예측하기 쉽지 않을 것 같습니다. 로렌츠가 당황할만 하지요.
우리나라는 그런 점에서 날씨 예보에 굉장히 불리한 지역입니다. 일단 인구밀도가 매우 높고, 덕분에 고층건물도 굉장히 많죠. 또한 국토의 70%가 산이기도 합니다. 이 산과 고층건물들은 공기의 흐름에 영향을 많이 주는 변수들이지요. 북한에 위치한 산맥들도 당연히 우리나라 기상에 영향을 주지만, 북한과의 기상 자료 교류가 이루어지고 있다는 말은 들어본 적이 없습니다.
또한, 기상 관측을 정확히 하려면 기상 자료가 많이 축적돼 있어야 하는데, 우리나라의 기상 관측이 시작된 건 1904년으로 100년이 조금 넘었지만 일제강점기와 여러 역사적인 사정들 때문에 50년 이상 기상자료가 축적된 곳은 거의 없다고 합니다.
하지만 한편으로는 우리가 안 좋은 상황을 긍정적인 상황보다 좀 더 많이 기억하는 성향도 무시할 수 없습니다. 일기예보가 들어맞아 편한 하루를 보낸 것보다는 일기예보가 틀려서 휴가를 망치거나 난데없이 비를 맞는 상황을 좀 더 강렬하게 기억하곤 하죠. 그래서 실제보다 일기예보가 자주 틀린다고 생각하는 것일 수 있습니다. 기상청에서 공식적으로 발표하는 강수 예보 정확도는 놀랍게도 92%에 달하니까요. 물론 저도 저 통계를 완전히 믿지는 않지만 생각보다 일기예보가 정확한 것일 수도 있습니다. 아마도요.
서울대학교 응용생물화학부 18학번 강지희(rkdwlgml0306@naver.com)
이웃집 필진

