[연재순서]
앞서 설명한 소행성의 모습을 구하는 4가지 방법(탐사선 직접 방문, 전파망원경 레이다 관측, 대형망원경 적응광학계 활용, 엄폐현상)은 모두 비용, 관측 기기 및 기회 등의 측면에서 제한적일 수밖에 없다. 하지만 이러한 한계를 모두 뛰어넘는 매우 효율적인 방법이 한 가지 있는데 바로 광도곡선 역산법(lightcurve inversion method)이다. 일반적으로 소행성은 고구마나 감자처럼 매우 불규칙한 모습을 가지고 있다. 또한 지구나 태양계 다른 행성들처럼 저마다의 자전축을 중심으로 자전을 하고 있다. 아래 그림처럼 불규칙한 모습을 가진 소행성의 자전은 시간에 따라 태양빛을 반사해서 우리에게 보이는 단면적의 변화를 가져오게 되는데 이를 광도곡선, 즉 시간에 따른 밝기 변화라고 한다.
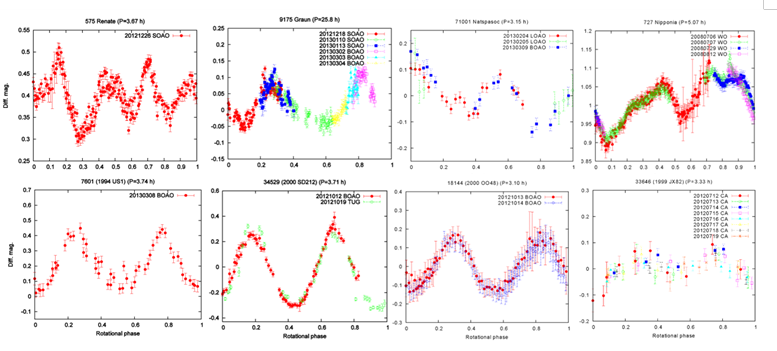
만약 소행성이 완벽한 공 모양이라면 자전에 따른 밝기변화는 나타나지 않을 것이다. 하지만 모든 소행성은 조금이라도 찌그러진 모습을 가지고 있으며 똑같이 생긴 소행성이 하나도 없다. 이로 인해 소행성의 광도곡선 또한 아래 그림처럼 제각각이다. 다시 말하면 우리는 소행성 광도곡선의 형태를 보고 소행성의 모습과 자전 상태를 유추할 수 있다. 예를 들면 길쭉하게 찌그러진 소행성일수록 가장 밝을 때와 가장 어두울 때의 밝기 차이가 클 것이고, 공에 가까운 소행성은 최대, 최소 밝기 차이가 작을 것이다. 바로 이것이 광도곡선 역산법의 개념이다. 또한 소행성의 광도곡선이 한 번의 자전주기에서 나타나는 모습으로 계속 반복되는 즉, 지구처럼 자전축이 고정돼 있는 소행성이 있는 반면, 광도곡선이 하나로 겹쳐지지 않는 텀블링 운동을 하는 비주축자전(non-principal axis rotation) 소행성이 있다.
이러한 광도곡선을 최소 3-4번의 소행성 출현(apparition)2) 기간 동안 획득하게 되면 광도곡선 역산법을 수행하기 위한 데이터가 모아지는 것이다. 광도곡선 역산법의 순서와 원리는 간단히 다음과 같은 3단계로 진행된다. 첫째 형상을 구하고자 하는 소행성의 광도곡선을 모두 합쳐서 하나의 자전주기를 결정한다. 이때의 자전주기는 우리에게 보이는 면이 같아지는 회합자전주기(synodic rotation period)가 아닌 항성자전주기(sidereal rotation period)여야 한다3). 즉, 소행성이 멀리 있는 별을 기준으로 스스로 한 바퀴 도는 시간을 결정한다.
광도곡선 역산법의 두 번째 순서는 자전축 방향 결정인데, 지구나 화성처럼 자전축이 기울어져 있는지, 수성이나 목성처럼 자전축이 황도평면에 수직하게 세워져 있는지에 따라서 광도곡선의 차이가 생기기 때문이다. 소행성의 자전축 방향은 황도좌표계인 황위와 황경 방향으로 표현하는데 자전축 방향 결정을 위해서는 보통 황위와 황경을 1도씩 나누어 계산했을 때 3축 타원체 소행성의 모델과 관측치의 사이의 오차가 최소가 되는 지점을 결정한다. 아래 그림은 소행성 파에톤(Phaethon)의 자전축 방향 결정의 예를 보여주는데, 그림에서 x축은 자전축 방향의 황경값, y축은 황위값을 나타낸다. 그림에서 카이(chi) 제곱의 값이 최소가 되는 위치인 황경 308도, 황위 –52도 부근이 소행성 파에톤의 자전축 방향을 나타낸다.

마지막 세 번째 소행성의 표면을 여러 개의 작은 면(facet)으로 나눈 뒤 앞서 결정된 자전주기와 자전축 방향을 각 면들이 태양빛을 반사해서 우리에게 보이는 밝기의 총합이 실제 관측을 통해서 얻은 광도곡선의 밝기와 비슷한 조건의 소행성 모델을 만드는 것이다. 이 단계에서는 한 가지 가정이 필요한데, 그것은 소행성은 볼록한 다면체(convex) 모델이라는 것을 기본으로 한다. 즉, 소행성 표면에서 가운데가 오목하게 폭 들어간 모양(concave)이 없다는 것을 가정하는데 물론 이는 우리가 탐사선 방문으로 알고 있는 실제 소행성의 표면 모습과는 다르다. 하지만 광도곡선 역산법을 통한 소행성의 형상과 자전축 방향 정보는 볼록한 다면체 모델만 고려하더라도 실제 소행성의 모습과 비슷하게 구현이 가능하며 또한 오목한 다면체 모델을 고려하게 될 경우 오목하게 들어가게 된 모양으로 인해 생긴 그림자와 실제 소행성 표면에서 구성물질의 차이로 인해 어둡게 나타나는 부분과의 구별이 광도곡선에서는 불가능하기 때문이다.
이러한 광도곡선 역산법을 통하여 지금까지 2,400여개가 넘는 소행성에 대해서 형상 모델이 구현됐다. 이는 '소행성 형상 구하기 (1)편'에서 소개한 4가지 방법을 모두 합친 숫자보다 자릿수(order of magnitude)가 차이나는 것이다. 이 모델들은 모두 체코 까를대학(Charles University) 수학 및 물리천문학부에서 운영하는 다밋(DAMIT: Database of Asteroid Models from Inversion Techniques) 웹페이지5)에 잘 정리돼 있다.

사실 소행성 광도곡선 역산법 알고리즘과 계산법을 최초로 개발한 사람은 천문학자가 아니다. 그는 응용수학 분야에서 세계 최고의 전문가인 핀란드의 미코 카살라이넨(Mikko Kaasalainen) 교수이다. 그는 수학자이면서 동시에 천문학 특히 소행성의 광도곡선을 이용한 형상 모델 재건(reconstruction)에 많은 관심을 가지고 있었다. 그 이유는 광도곡선 데이터(data)만 가지고 대상(object)의 정량적 성질, 즉 소행성의 형상을 만들어 내는 것이 바로 수학 및 과학 분야에서 가장 중요한 문제 중 하나인 역문제(inverse 혹은 reverse problem)를 푸는 것이기 때문이다6).
또 다른 예로는 우리가 측정하는 지진파 데이터를 가지고 지구 내부 구조를 만들어 내는 것이나 의료장비인 CT 촬영을 통해 신체조직의 내부 밀도 영상을 보여주는 것 역시 역문제를 푸는 것으로 생각하면 쉽다. 카살라이넨 교수는 1990년도 헬싱키 대학의 석사학위 논문으로 소행성의 밝기 변화를 기반으로 소행성의 형상을 구하는 방법을 발표하였고, 이를 기반으로 1992년도 천문학 및 천체물리학(Astronomy and Astrophysics) 저널에 소행성 광도곡선 역산법을 처음으로 소개하는 <대기가 없는 천체의 광도곡선 해석(Interpretation of lightcurves of atmosphereless bodies)>라는 제목의 2편의 시리즈 논문을 발표한다7). 이후 1994년도에 옥스퍼드 대학에서 박사학위 를 받은 뒤8), 1990년대 후반 다시 헬싱키 대학으로 돌아와 2001년도 9월, 드디어 <소행성 광도곡선 역문제를 풀기위한 최적의 방법(Optimization methods for asteroid lightcurve inversion)>라는 제목의 시리즈 논문 2편을 행성과학 분야 전문 저널인 이카루스(Icarus)에 발표한다9). 첫 번째 시리즈 논문 초록의 첫 번째 문장은 아래와 같이 시작한다.
우리는 소행성 광도곡선으로부터 형상, 자전 주기, 그리고 자전축 방향 등을 결정하는 새로운 방법을 개발했다.
We have developed new methods for determining the shapes (and albedo distributions), rotation periods, and pole directions (as well as other parameters, e.g., those of the scattering law) of asteroids from their lightcurves.
당시 36살이었던 젊은 수학자가 쓴 이 논문은 현재까지도 여전히 그리고 앞으로도 전 세계에서 소행성 광도곡선 관측자들뿐만 아니라 소행성 형상 모델링 관련 연구자들이 가장 많이 인용하는 논문이 됐다.10)
소행성 광도곡선 역산법, 즉 소행성 광도곡선을 통한 형상 구하기
이 역문제를 푸는 것은 사실 위에서 언급한 복잡한 단계를 떠나서 소행성이 지구에서 관측할 때 보이는 면에 대한 정보를 종합하여 그 형상을 재구성(reconstruction) 하는 개념으로 생각하면 쉽게 이해할 수 있다. 그러나 아래 그림에서도 볼 수 있듯이 단 한 번의 관측으로는 우리에게 보이는 소행성의 어떤 면인지(북반구인지, 남반구인지 조차도) 구분하기가 불가능하다. 또한 소행성의 두 번째 출현 시기에 관측을 진행하여도 태양-소행성-지구가 이루는 관측 기하학(geometry)과 소행성의 자전축 방향과의 관계로 인하여 이전과 같은 면(북반구 혹은 남반구)을 또다시 관측하게 될 가능성이 있는 것이다. 따라서 앞서 설명한 것처럼 정확한 소행성의 형상을 얻기 위해서는 최소 3-4번의 소행성 출현 기간 동안의 광도곡선이 필요하다. 마치 엑스-레이 촬영으로 잘 보이지 않는 질병이 CT 촬영(컴퓨터단층 촬영)으로 분명하게 보이는 것과 같은 원리다.

하지만 이렇게 소행성의 3-4번의 출현을 통한 관측기회를 기다리는 것은 사실 거의 10년에 가까운 기간 동안 광도곡선을 얻어야 겨우 1개의 소행성의 형상 모델을 완성한다는 것을 의미하기에 무척 시간이 오래 걸리는 작업이다. 이에 최근에는 촘촘한(dense) 광도곡선 데이터만 이용하던 기존 방식에 덧붙여 소행성 발견을 위한 혹은 궤도를 구하기 위한 탐사 관측 자료, 즉 하룻밤에 2-3개의 관측만 이루어진 듬성듬성한(sparse) 관측 데이터를 함께 이용해서 형상을 구하는 방법 또한 활발히 진행되고 있다.

글: 김명진(연세대학교 천문우주학과 이학 박사)
現 한국천문연구원 우주위험감시센터 선임연구원
前 한국천문연구원 행성과학그룹 박사후연구원
##참고자료##
1) 마리아(Maria) 소행성 종족 관측 결과 발표 천문학 저널(Astronomical Journal) 논문. Kim, M-J., et al. "Rotational properties of the Maria asteroid family" The Astronomical Journal 147.3 (2014): 56.
2) 소행성은 태양-소행성-지구가 만드는 각도에 따라서 지구에서 관측이 가능한 기간이 있는데 이를 출현(apparition)이라고 한다. 소행성대 소행성의 경우 보통 1-2년에 한번 씩 관측 가능한 기간이 돌아온다.
3) 회합자전주기와 항성자전주기는 태양일과 항성일의 차이가 나는 개념과 비슷하다.
4) 소행성 파에톤의 광학관측 특성에 관한 논문. Kim, M-J., et al. "Optical observations of NEA 3200 Phaethon (1983 TB) during the 2017 apparition" Astronomy and Astrophysics 619, A123 (2018)
5) https://astro.troja.mff.cuni.cz/projects/damit/
6) 이와는 반대로 대상(object)으로부터 실험(관측)을 통해 정보(data)를 직접 얻어내는 것을 정문제(direct 혹은 forward problem)를 푼다고 말한다. 즉 소행성 관측을 통해 광도곡선을 얻어내는 방법도 이에 해당한다.
8) 박사학위 논문제목 <On the construction of invariant tori and integrable Hamiltonians>
9) 논문 시리즈 1편. Kaasalainen, M. & Torppa, J. “Optimization Methods for Asteroid Lightcurve Inversion. I. Shape Determination” Icarus 153, 24 (2001)
논문 시리즈 2편. Kaasalainen, M. et al. “Optimization Methods for Asteroid Lightcurve Inversion. II. The Complete Inverse Problem” Icarus 153, 37 (2001)
10) 애석하게도 미코 카살라이넨 교수는 오랫동안 암으로 투병하다 지난 2020년 4월 12일 55세를 일기로 세상을 떠났다. 그는 2009년도부터 핀란드 탐페레 대학(University of Tampere)의 수학과 교수로 재직했으며 핀란드 역문제 관련 연구 센터(Finnish Centre of Excellence in Inverse Problems Research)의 수장으로 여러 해 동안 이 분야의 세계적인 권위자로 활동했다. 그의 수학과 과학에 대한 통찰력과 소행성 형상 모델링 방법의 정립으로 인한 태양계 형성과 진화에 대한 이해의 증진은 앞으로도 영원히 그의 업적으로 남을 것이다.
11) 소행성 7968 엘스트-피자로(Elst-Pizarro)의 활동성과 자전축 방향에 관한 논문. Toth, I. "Search for comet-like activity in asteroid 7968 Elst-Pizarro and limitation of its rotational pole orientation" Astronomy and Astrophysics 446, 333-343 (2006)


