와류(Vortex)[1]가 안정적으로 존재한다는 사실이 수학적으로 밝혀졌습니다. 기상 예측 기술 등 기상이변을 예측하는데 도움이 될 수 있습니다.
UNIST 수리과학과 최규동 교수는 둥그런 공 모양의 와류가 안정적인 상태로 존재한다는 사실을 수학적으로 증명에 성공했습니다.
와류는 공기나 물로 이뤄진 유체 내부에 회전의 영향을 강하게 받는 영역인데요. 우리가 뉴스에서 쉽게 접할 수 있는 태풍, 토네이도 현상이 와류 현상 중 하나입니다.
최 교수가 수학적으로 증명한 `특정 와류가 안정적 상태이다‘라는 것은 일반적으로 우리가 현실에서 만날 수 있는 공기나 물의 흐름에서도 특정 형태의 와류가 관측되고 존재한다는 것을 말합니다.
유체역학에서는 1757년에 만들어진 오일러 방정식으로 와류의 흐름을 주로 계산해왔습니다. 유체역학에서 이상적인 유체의 흐름을 기술하는 데 사용되는 오일러 방정식은 200년이 넘게 수학/물리학(유체역학)에서 연구되어 온 주제입니다. 이 비선형 방정식은 실제로 손으로 풀 수 있는 방정식이 아니라서 일반적인 해 공식이 존재하지 않고 다만 몇가지 특수 해들의 존재만 오랫동안 알려져 왔습니다. 이렇게 알려져 있는 특수 해 중에 영국수학자 힐이 19세기 후반에 발견한 구형(spherical) 와류는 와류 영역이 정확하게 구 모양이고 구 밖에서는 소용돌이도(vorticity)[2]가 사라진다(curl-free)는 점에서 독특합니다.
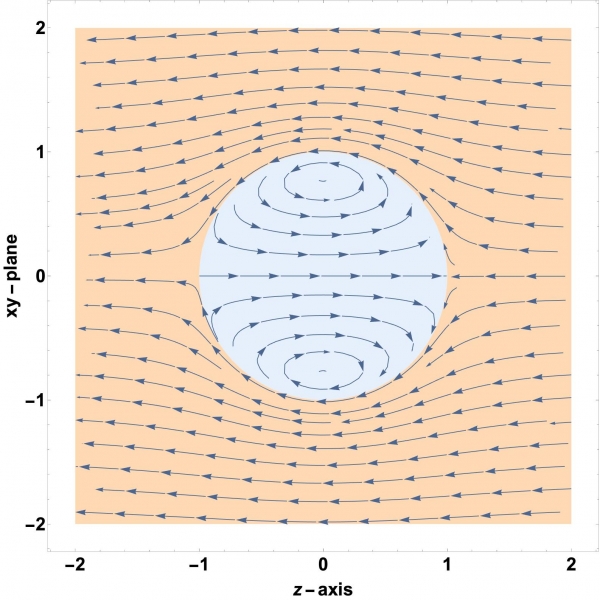
최 교수는 변분법[3]을 이용해 힐이 계산한 구형 와류가 특정 조건에서 운동에너지를 최대화함을 확인했는데요. 수학 해석 분야에서 사용되는 함수해석학, 편미분방정식이론 등을 도입해 기존에 연구됐던 2차원 유체의 흐름을 넘어 축대칭 조건을 포함한 3차원적 유체의 흐름까지 계산할 수 있도록 필요한 이론들을 한 단계 발전시켰습니다.
힐이 발견한 구형 와류의 진행 앞면에는 강하게 상승하는 기류가 존재한다. 이 상승기류는 태풍이나 토네이도 등에서도 쉽게 확인 가능한데, 최 교수의 연구는 이런 상승기류들의 잔류시간을 측정하는 등 다양한 연구의 시발점으로 활용될 수 있습니다.
최규동 수리과학과 교수는 “그동안 중단됐던 와류의 안정성에 대한 연구가 국제적으로 더욱 활발해지고 있다”며 “기상이변 등이 많아지는 오늘날의 기상 예측 기술발전에 장기적인 관점에서 도움을 줄 것으로 기대된다”고 전했습니다.
연구 결과는 수학 학술지 '순수-응용수학저널(Communications on Pure and Applied Mathematics)'에 7월 24일 온라인 게재됐습니다.
논문명: Stability of Hill's spherical vortex
#용어설명
1. 와류(vortex)
흔히 소용돌이라고도 부르는 와류는 소용돌이도(vorticity)가 집중적으로 존재하는 영역을 뜻한다.
2. 소용돌이도(vorticity)
소용돌이도는 유체의 속도함수에 미분연산자를 외적을 취함으로 얻어지는 벡터 함수이다. 이 값이 뜻하는 것은 이 값을 구하는 점 근방에서 국소적(local)으로 영역이 회전하고 있는 정도와 방향을 나타낸다.
3. 변분법
에너지 또는 거리가 최소가 되거나 최대가 되게 하는 곡선이나 속도 등을 찾는 방법이다

